Use elimination to solve for x and y And they gave us two equations here x plus 2y is equal to 6 and 4x minus 2y is equal to 14 So to solve by elimination, what we do is we're going to add these two equations together so that one of the two variables essentially gets2x – y = 3 ii 3x – 4y = 7 ;Xy=5;x2y=7 Try it now Enter your equations separated by a comma in the box, and press Calculate!

Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6
3-(x-5)=y 2 2x y)=4-3y by elimination method
3-(x-5)=y 2 2x y)=4-3y by elimination method-To find y we substitute x = 1 into (1) and solve for y 2(1)3y=5 3y = 2 5 3y = 3 y = 1 Check the answers in the 2nd equation 3x(2y3)/5=4 3(1) (2(1)3)/5 = 4 3 (5)/5 = 4 3 (1) = 4Subtract both the equation => (6x 4y) (6x 9y) = 22 12 => 6x 4y 6x 9y = 10 => 5y = 10
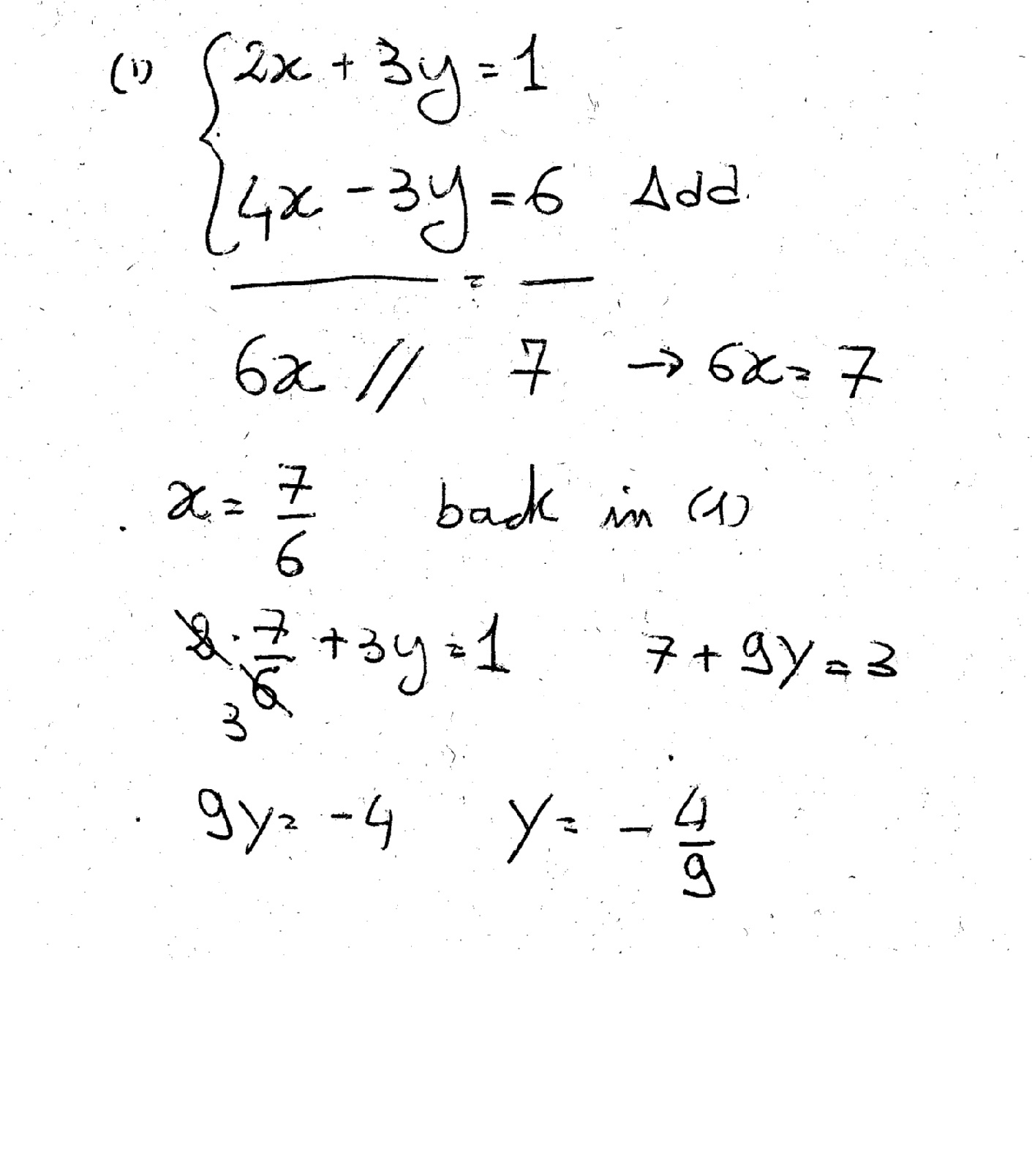



How Do You Solve The System Using The Elimination Method For 2x 3y 1 And 4x 3y 6 Socratic
The substitution method is most useful for systems of 2 equations in 2 unknowns The main idea here is that we solve one of the equations for one of the unknowns, and then substitute the result into the other equationStep 1 Solve any one of the equations either x = or y = Step 2 Substitute the value that we got from step 1 in the other equation Step 3 Now we have got the value of any one of the variables x or y Step 4 Apply this value in step 1 in order to get the value of other variableSolve 2xy=4 , 3yx=3 graphically and also , find the coordinates of the points where these lines intersect the 2 axis Report Posted by Pranjal Chaudhary 5 months ago
Equation (1) can be written as 2x = 9 – 3y x = (9 – 3y)/ 2 (3) By substituting the value of x in equation (2) 3 × (9 – 3y)/ 2 4y = 5 By further calculation (27 – 9y)/ 2 4y = 5 By taking LCM NCERT Solutions for Class 10 Maths Chapter 3 Exercise 34 Question 1 Summary On solving the pair of equations by the elimination method and the substitution method we get x, y as (i) x y = 5 and 2x 3y = 4 where, x = 19/5, y = 6/5 , (ii) 3x 4y = 10 and 2x 2y = 2 where, x = 2, y = 1 , (iii) 3x 5y 4 = 0 and 9x = 2y 7 where, x = 9/13, y = 5/13, (iv) x/2 2y/3 = 1 andFree equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps Type in any equation to get the solution, steps and graph
Solve each of the following pairs of equations by the elimination method Solve by elimination method 3 x 4 y = − 4 5, 2 x − 3 y = 6 3x – y = 2 ; If the linear equation in two variables 2x –y = 2, 3y –4x = 2and px–3y = 2are concurrent, then find the value of p If ܽa b = 35 and a − b = 13, where a > b, then find the value of a and ܾb Solve the system of linear equations by elimination method 2/3x3/4y=1/12;3x/42/3y=1/2




7 X 5 2x Y 4 3y 5 5y 7 2 4x 3 6 18 5x Solve Using Cross Multiplication Brainly In
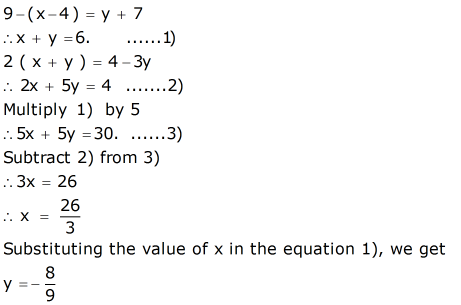



9 X 4 Y 7 2 X Y 4 3y Mathematics Topperlearning Com 5inhk66
Question Need help solving system by elimination method x/2 y/3 = 7/6 2x/3 3y/4 = 5/4 Thank you Found 3 solutions by Alan3354, Fombitz, rothausercFor solving pair of equation, in this exercise use the method of elimination by equating coefficients 3 (x 5) = y 2 2 (x y) = 4 3y Advertisement Remove all ads Solution 3 (x 5) = y 2 ∴ 3 x 5 = y 2 ∴ x 8 = y 2 ∴ x y = 6 (1) 2 ( x y ) = 4 3y ∴ 2x 2y = 4Weekly Subscription $249 USD per week until cancelled Monthly Subscription $799 USD per month until cancelled Holidays Promotion Annual Subscription $1999 USD for 12 months (40% off)
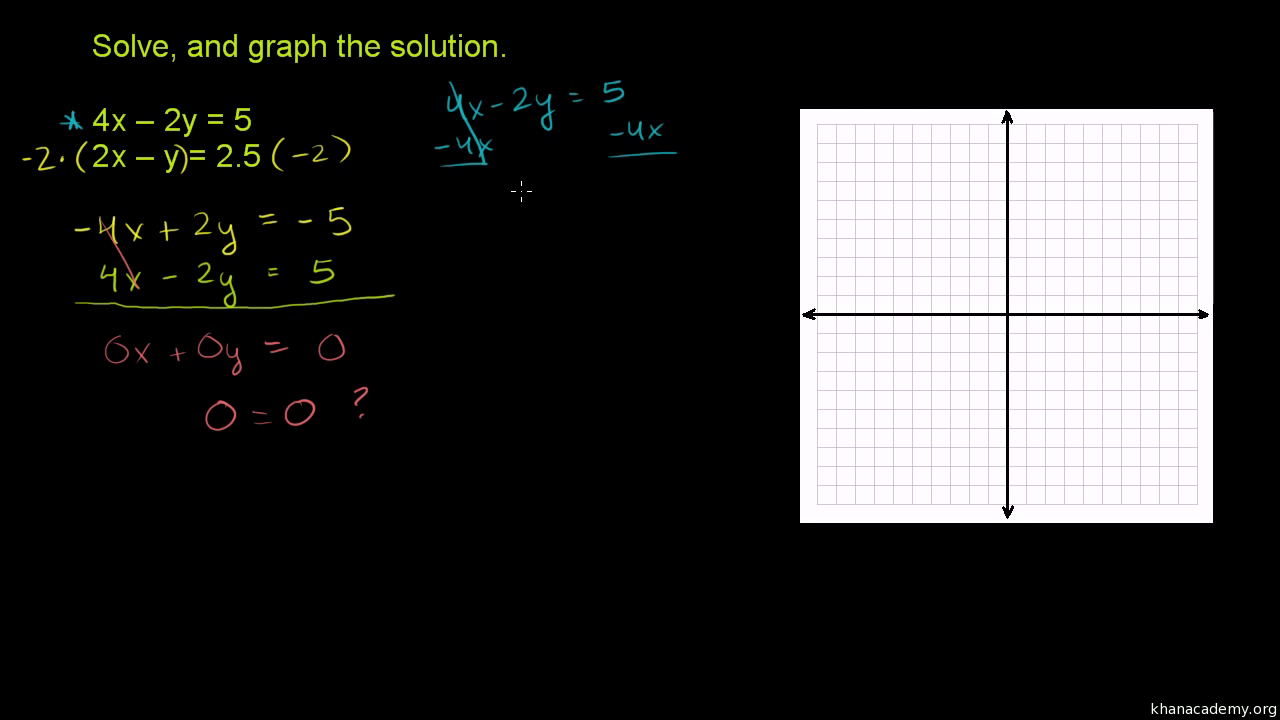



Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy
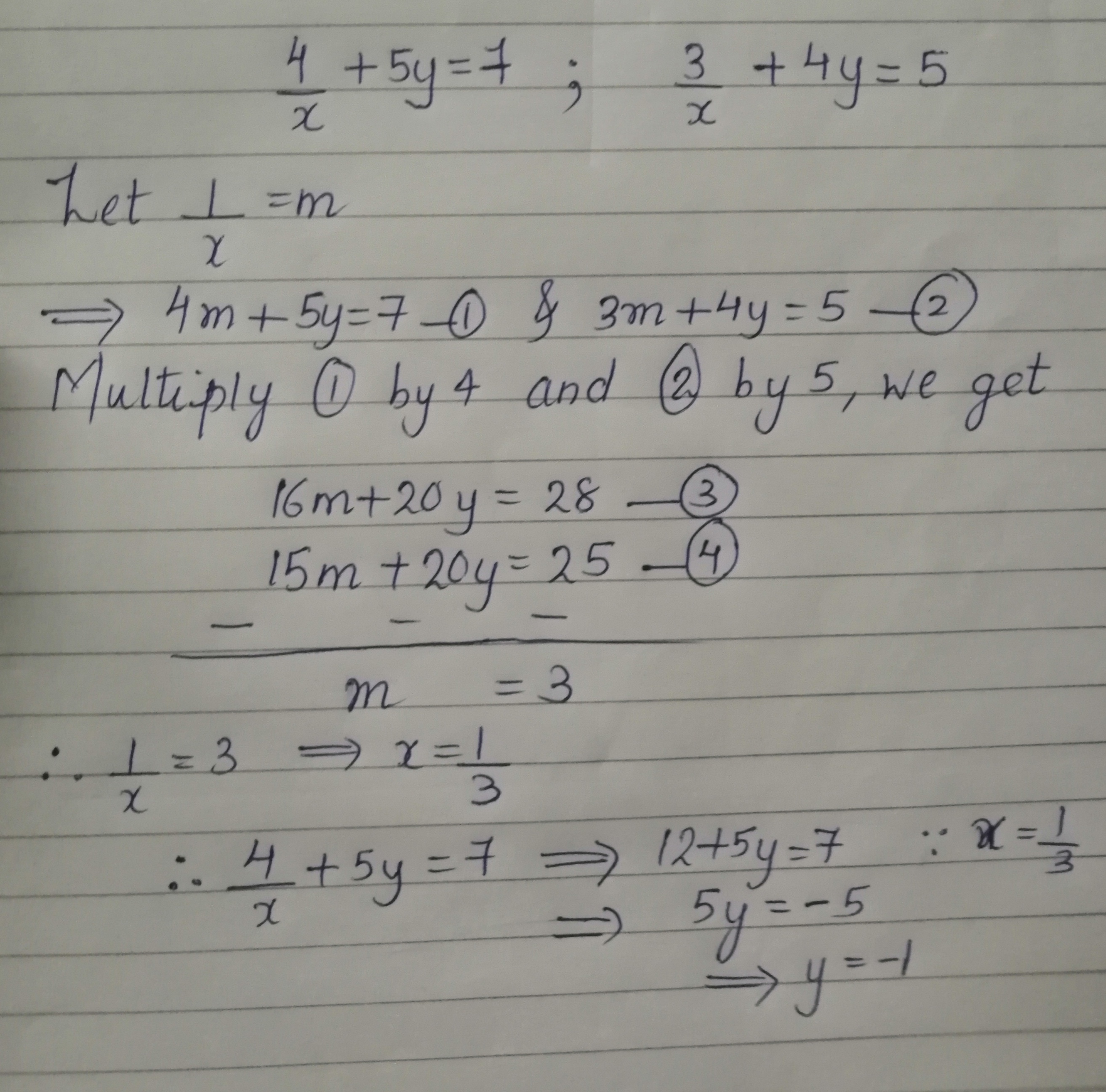



4 X 5y 7 3 X 4y 5 Mathematics Topperlearning Com Eyz2xh55
To make it Simpler for you, Consider the Following Example Solve this set of equations 2x y = 4 and 5x – 3y = 1 using elimination method The equations given are 2x y = 4 (i) 5x – 3y = 1 (ii) Multiplying equation (i) by 3, you get, {2x y = 4} {× 3}Solving systems of linear equations using Gauss Seidel method calculator Solve simultaneous equations 2xyz=5,3x5y2z=15,2xy4z=8 using Gauss Seidel method, stepbystep online We use cookies to improve your experience on our site and to show you relevant advertisingAnswer (1 of 3) The trick with Gaussian elimination is to find the leading element (circled) at from the starting matrix and new matrix at each step This will give us an upper triangular matrix in Row Echelon form Then we can reduce further down to Reduced Row Echelon Form Note that



Solve The Following Systems Of Linear Equations By Gaussian Elimination Method I 2x 2y 3z 2 X 2y Z 3 3x Y 2z 1 Sarthaks Econnect Largest Online Education Community




Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6
Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank you x = 1/2 , y = 1/3 Solution Here , The given equations are ;3y – x = 4 asked in Linear Equations in Two Variables by KomalKumari ( 490k




Solving A System Of Equations Using A Matrix Precalculus Socratic




If 3x 2y 5 And 3y 2x 3 Then Find The Value Of X Y Scholr
Or click the example About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding orSubstitute 4 for x in either x – 3y = 7 original equation Then solve for y 4 – 3y = 7 – 3y = 3 3y = 3 3 3 y = –1 Use elimination to solve each system of equations 1 2x 2y = –2 2 4x – 2y = –1 3 x – y = 2 3x – 2y = 12 –4x 4y = –2 x y = –3 ( , ) ( , ) ( , ) 4 6x 5y = 4 5 2x – 3y = 123/2x 2/3y = 5 (1) 5/x 3/y = 1 (2) Eq(1) can be rewritten as ;




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3



無料ダウンロード 3x 2y5 X5 Y
The simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematicallyAnswer (1 of 4) 2 algebraic methods (elimination and substitution) and graphical method Elimination 2x 3y = 5 So 6x 9y = 15 (equation 1) 3x y = 4 6x 2y = 8 (equation 2) (6x 9y) (6x 2y) = 15 8 7y = 7 y = 1 (equation 3) Substitute y = 1 into equation 2, 3x (1) = 4 x =Example 1 2x 3y = –2 (equation 1) 4x – 3y = 14 (equation 2) Solution Step 1 In this example the coefficients of y are already opposites (3 and –3) Just add the two equations to eliminate y Step 2 Isolate variable x 6x = 12 Step 3 To get the value of y you need to use the substitution method




99以上 X Y 5 2x 3y 5 2 3x Y 5 2x 3y 5 X 2y 4y 16
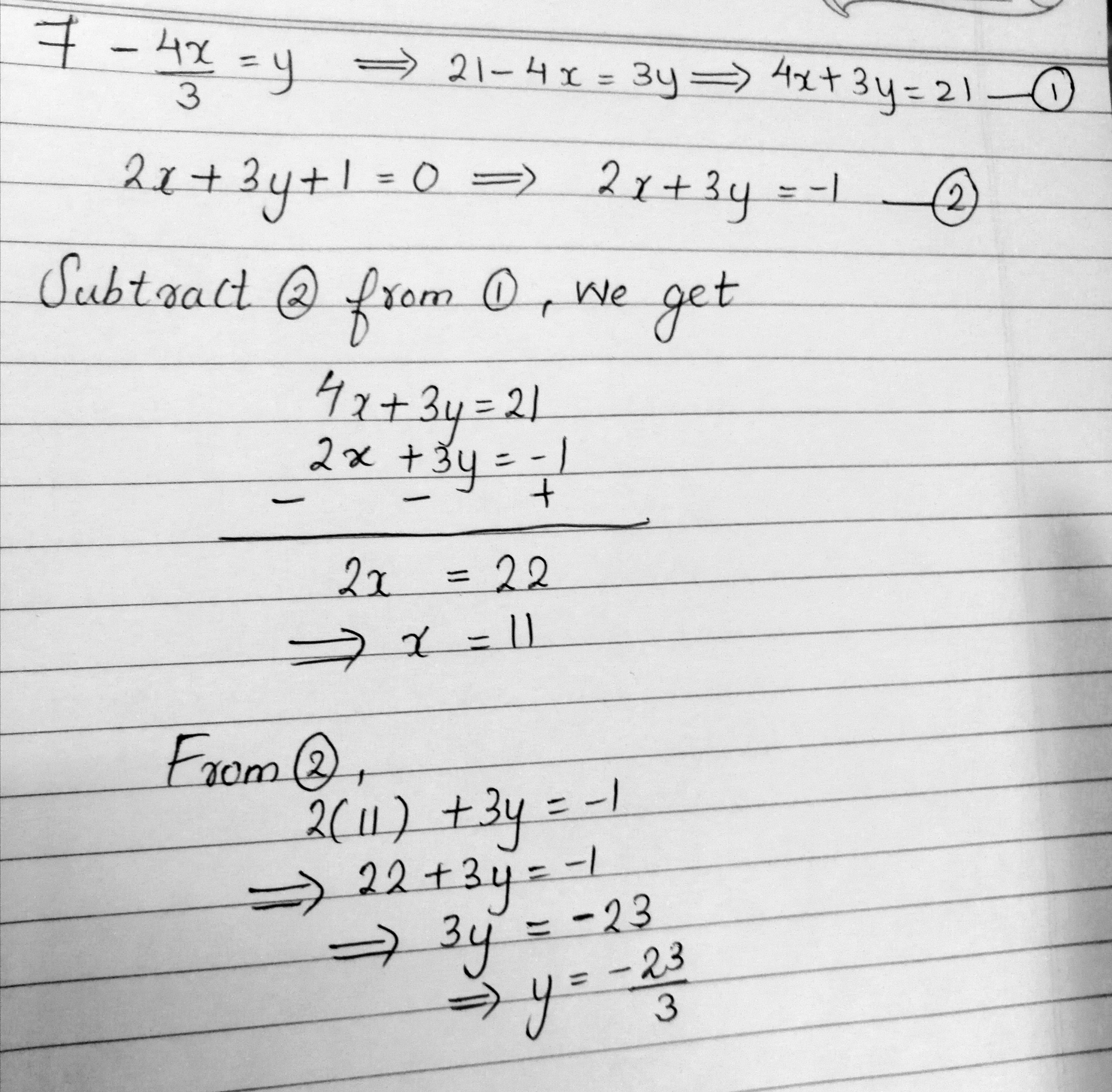



7 4x 3 Y 2x 3y 1 0 Mathematics Topperlearning Com Iwb1egg
19y = 22 3x 4y = 6 6x 8y = 10 The system shown has _____ solution (s) no 3x 5y = 78 2x y = 0 The point of intersection of the5x – 2y = 0 iii 2x – 3y = 4 ;Algebraic method You can solve simultaneous equations by adding or subtracting the two equations in order to end up with an equation with only one unknown value




Solved Please Help Me Answering The Following Problems 18 Chegg Com




Notes For Systems
The following steps will be useful to solve system of linear equations using method of substitution Step 1 In the given two equations, solve one of the equations either for x or y Step 2 Substitute the result of step 1 into other equation and solve for the second variable Step 3 x = 11/11 x = 1 now we have the value of x let's simply further for y let's take equation 2 5(1) 3y =1 5 3y = 1 51 = 3y 4 = 3y 4/3 = y to confirm your values you can put these values in one of the two equations given initially , let's use equation two to check 5x3y = 1 ( now let's place the values of x and y into the 3x2y=11;2x3y=4 solve by elimination method To find Find the value of x and y Solution 3x 2y = 11 (i) 2x 3y = 4 (ii) Multiply (i) by 2 and (ii) by 3 Multiply (i) by 2 and (ii) by 3so, the equation becomes 6x 4y = 22;



What Is The Answer To Find The Equation Of A Straight Line Through The Point Of Intersection Of Lines 2x 3y 5 0 And 3x 4y 7 0 Which Is Parallel To The Line 2x Y 2 0 Quora




Cross Multiplication Methed X Y 5 Amp 2x 3y 4 Brainly In
Solve the following pair of linear equations by the elimination method and the subsitution method 3 x − 5 y − 4 = 0 and 9 x = 2 y 7And y is equal to 3 And we can verify that it works in both equations In this top equation let me do it in a new color negative 3 times 3 plus 4 times 5 is this is negative 9 plus , which is, indeed, equal to 11 So both of these satisfy the first equation And then if we take the second equation, 3 plus 2 times 5, that's 3 plus 106x = 12 (guessed) Solve the system by the elimination




Solved 13 O O O O In Exercises 15 36 Solve The System Of Chegg Com




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection
Which of the following equations could be the result of multiplication and addition to eliminate a variable in the system of equations?=> 3/2x 2/3y = 5 => (9y 4x)/6xy = 5 => (9y 4x)/xy = 5•6 => 9/y 4/x = 30 (3) Now, Multiplying eq(2) by 4 , we get ; Use the Substitution method to solve the system of equations y 2x = 5 3y x = 5 Solve one of the equations for x or y Let's solve the first one for y y 2x = 5 y = 2x 5 Now let's substitute 2x 5 for y in the second math Elimination was used to solve a system of equations




Solve The Pair Of Linear Equations By Cross Multiplication Method 2 2x Y 5 3 X 3y 1 0 Brainly In
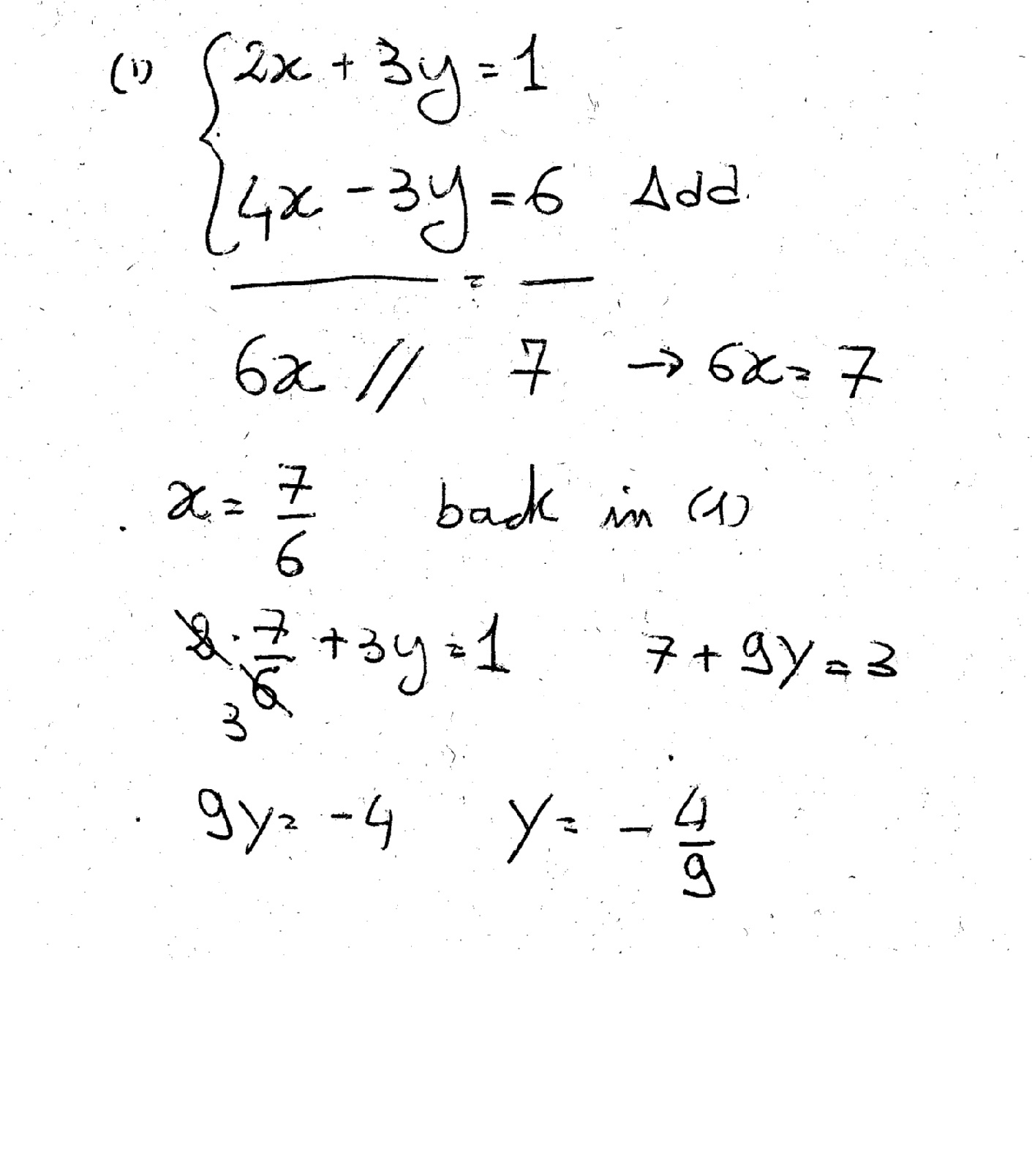



How Do You Solve The System Using The Elimination Method For 2x 3y 1 And 4x 3y 6 Socratic
x=3 y=2 On paper you should line the equations up, one below the other 2x3y=12 3x5y=1 In elimination, you have to find the least common multiple between one of the variables I prefer to eliminate x and solve for y first and so the least common multiple between 2x and 3x is 6x You'll have to multiply 2x3y=12 by 3 and 3x5y=1 by 2 6x9y=36 6x10y=2 Now you haveSolve the system by the elimination method 2x y 4 = 0 2x y 4 = 0 When you eliminate y, what is the resulting equation?6x 9y = 12;




Ex 3 4qno1 1 Solve X Y 5 2x 3y 4 By The Elimination Method Youtube




99以上 X Y 5 2x 3y 5 2 3x Y 5 2x 3y 5 X 2y 4y 16
x = 1 y = 2 Ok So prefer the elimination method, but you can do this with substitution as well First put the equations on top of each other x 2y= 5 2x3y=4 Then find the variable that would be easiest to cancel out I think it's x because you only have to modify one of the equations Let's multiply the first equation by 2 This will allow us to cancel out the two x's in the equations Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient 2x y = 13, 5x – 3y = 16 asked in Linear Equations in Two Variables by HarshKumar ( 327k points)Selina solutions for Concise Mathematics Class 9 ICSE chapter 6 (Simultaneous (Linear) Equations (Including Problems)) include all questions with solution and detail explanation This will clear students doubts about any question and improve application skills while preparing for board exams The detailed, stepbystep solutions will help you understand the concepts better and clear your




3 X 5 Y 2 2 X Y 4 3y Brainly In



How To Use System Of Equations To Solve 2x 3y 25 And 3x 3y 25 Quora
Solution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0 Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving (3) and (2) by Elimination –5y = –6 5y = 6 y = 𝟔/𝟓 Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 × 5 − 6)/5 x = (25 − 6)/5 x = 𝟏𝟗/𝟓Do the arithmetic x=9,y=2 Extract the matrix elements x and y \frac {1} {3}x5y=13,2x\frac {1} {2}y=19 In order to solve by elimination, coefficients of one of the variables must be the same in both equations so that the variable will cancel out when one equation is subtracted from the other




X 3y 6 0 2x Y 5 By Elimination Method Brainly In




Solve The Following Pair Of Linear Equations By The Elimination Method And The Substitution Method X Y 5 And 2x 3y 4
=> 4•(5/x 3/y) = 1•4 => /x 12y = 4 (4) Now,4x = 8 1) 2x y = 3 Solve the system by the elimination method 2x 3y 10 = 0 4x 3y 2 = 0 When you eliminate y, what is the resulting equation? the some of the numerator and denominator of a fraction is 2 more than twice the numerator if the numerator and the denominator are reduced by 3 thay are in ratio 34 find the fraction 2x3Y13=0;3X5Y=16 stimulation method Xy=6 X
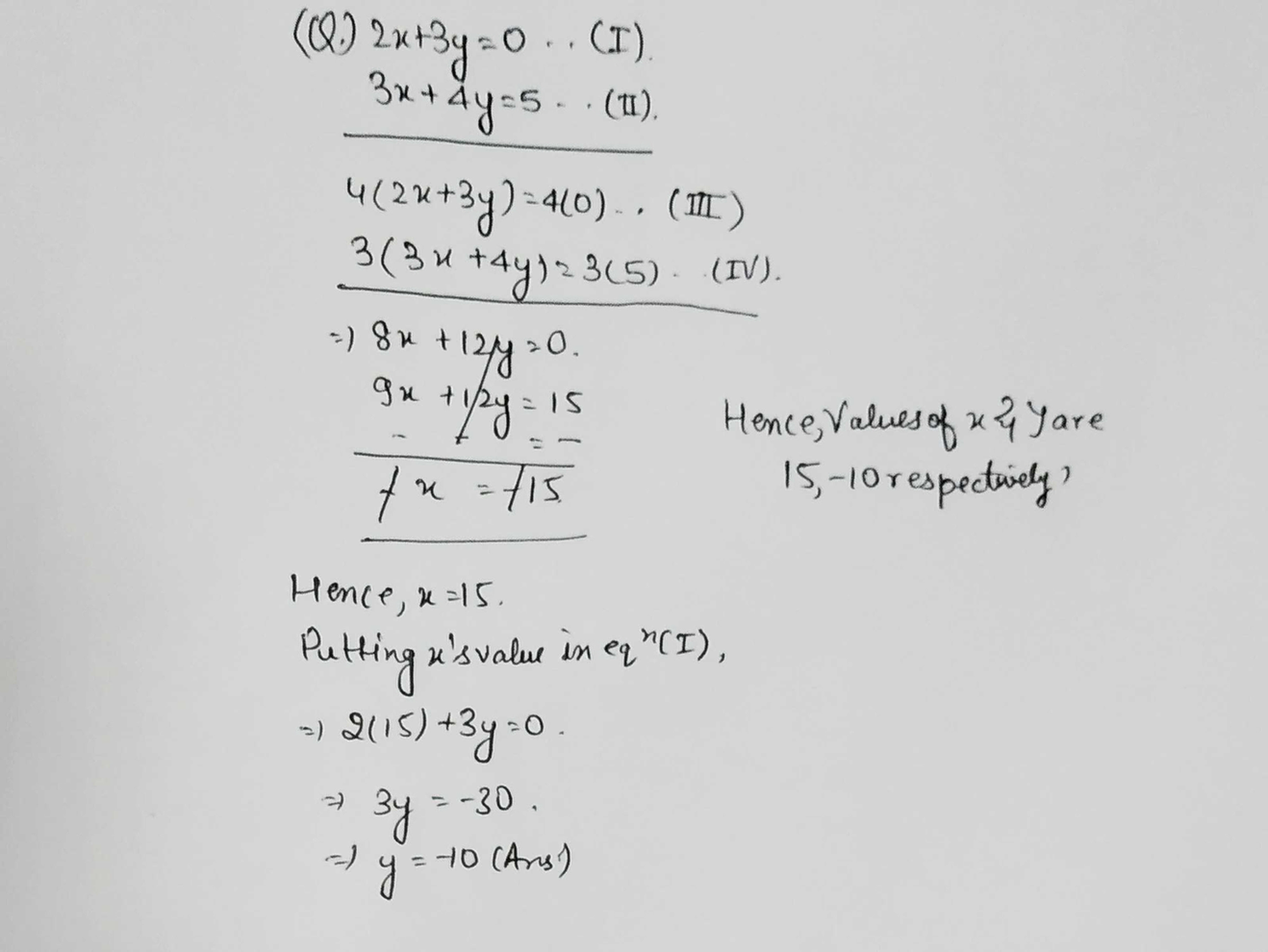



2x 3y 0 And 3x 4y 5 By Elimination Method Scholr




Elimination Method Day 2 Today S Objective I Can Solve A System Using Elimination Ppt Download
Solve the following system of equations by substitution First, we will solve the first equation for y y Now we can substitute the expression x − 5 x − 5 for y y in the second equation Now, we substitute x = 8 x = 8 into the first equation and solve for y y Our solution is ( 8, 3) ( 8, 3) Check the solution by substituting ( 8, 3) ( 8 Solve this system using elimination (3x5y=4) (2x6y=18) math Use elimination to solve each system of equations xy=3 2x3y=16 math solve the system by the elimination method 4x=5y24 5x=4y21 Algebra 2 Solve the system by elimination 2x 2y 3z = 0 2x y z =3 2x 3y 3z = 5 How do I do this?Solve those using the elimination method steps mentioned above and find the values of those 2 variables Substitute the values in any of the given equations to find the value of the third variable Let's solve three equations 3xy2z=5, 4x2yz=6, and 5x3yz=1 for a better understanding Now, we have found that x=1




Solved 8 Find The Inverse Of A 3 9 Solve The Following Chegg Com




Solve System Of Linear Equations Using Matrix Method 2x 3y 3z 5 X 2y Z 4 3x Y 2z 3 Mathematics Shaalaa Com
Look at the x coefficients Multiply the first equation by 4, to set up the xcoefficients to cancel Now we can find Take the value for y and substitute it back into either one of the original equations The solution is Example 3 Solve the system using elimination methodTo solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 3xy=2,2xy=3 3 x − y = 2, 2 x − y = 3 Choose one of the equations and solve itQuestion Solve using the substitution method, the elimination method, or the graphing method 5 2(xy) = 3x x, x = 3y 4 6 y = twofifths – 7, y = twofifths 4 I need help in solving these Answer by checkley77() (Show Source)




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora
Facebook Whatsapp Transcript Ex 63, 11 Solve the following system of inequalities graphically 2x y ≥ 4, x y ≤ 3, 2x – 3y ≤ 6 First we solve 2x y ≥ 4 Lets first draw graph of 2x y = 4 Putting x = 0 in (1) 2 (0) y = 4 0 y = 4 y = 4 Putting y = 0 in (1) 2x (0) = 4 2x = 4 x = 4/2 x = 2 Points to be plotted are (0, 4), (2 Find an answer to your question Use the elimination method to solve the system of equations 2x 3y = 8 x y = 9 spencerblack8 spencerblack8 Mathematics Middle School answered Use the elimination method to solve the system of equations 2x 3y = 8 x y = 9 2 See answers




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




If 3x 2y 24 And 2x 3y 18 Then Find X Y And X Y




Solve By Matrix Method 2x 3y 3z 5 X 2y Z 4 3x Y 2z 3



2




Use The Elimination Method To Solve The Following Systems Of Plainmath




3 6 Systems With Three Variables Ppt Video Online Download



If 2x 3y 17 And 3x 5y 27 What Are X And Y Quora




Tuesday September 23 14 Warm Up Put The Solve The System Using The Substitution Method 2x 5y 5 1 X 3y 3 2 Solution Step 1 Solve 2 For X X 3y 3 2 X 3y




X Y 5 And 2x 3y 4 Solve By Elimination Method Brainly In
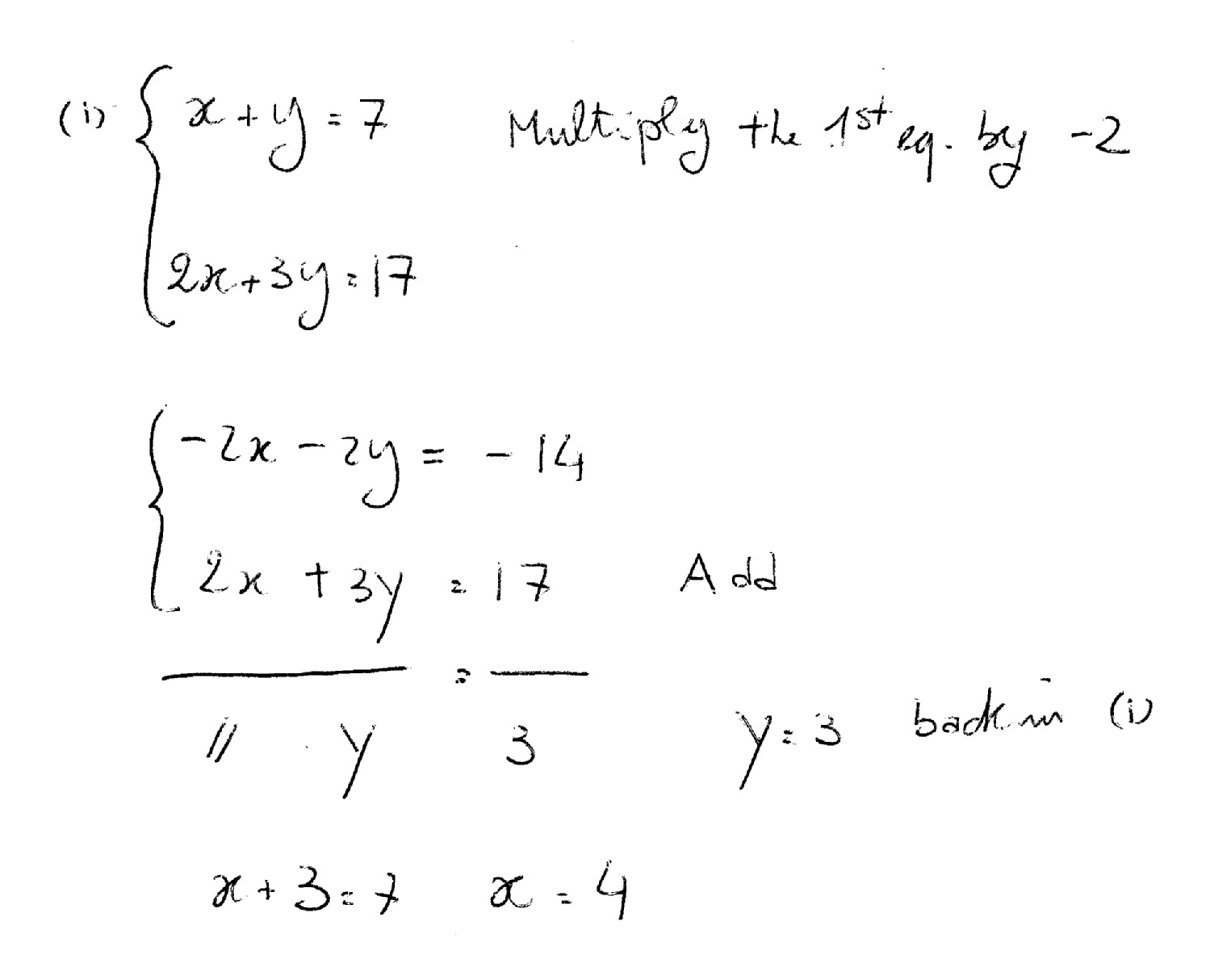



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic



Solve The Following Simultaneous Equations Graphically 2x 3y 4 3y X 4 Algebra Shaalaa Com



Is The Gauss Elimination Method X 2y 3z 1 2x 3y 8z 2 X Y Z 3 Quora




For A Pair Of Equations 2x 3y 10 And 3x Y 4 Find X




Solved Solve The Following Systems Of Linear Equation Using Chegg Com




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection



Solve The Following Linear System Of Equations Using Gauss Jordan Elimination Method 4 6 X 2y 3z 2 X 2y 3z 4 4 2x 3y 8z 7 5 X 3y Z 11 Course Hero




4 Solve The Following Linear System By Gauss Jordan El Itprospt




Solve These By Elimination Method 1 2x Y 4 And 5x 3y 1 2 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Elimination Method Day 1 Ppt Download




Solve The System Of Equations 2x 3y 17 3x 2y 6 By The Method Of Cross Multiplication



Systems Of Linear Equations




Omtex Classes 2x 3y 4 3y X 4 Solve The Following Simultaneous Equations Graphically




Solved 3 58 Solve The System By Using The Elimination Chegg Com




Answered Solve The Following System Of Equations Bartleby




Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy




Solve The Following Simultaneous Equations 3 X 5 Y 2 2 X Y 4 3y Use Elimination And The Cross Brainly In




Solved 1 Solve The Following Systems By Using The Chegg Com




2x 3y 4 0 3x Y 5 0 Youtube



How To Solve A Simultaneous Equation By Graphic Method X 3y 5 2x 4y 10 Quora




無料ダウンロード 3x 2y5 X5 Y




C Solve The Pair Of Equations Using Method Of Elimination By Equatingcoefficients 3 X 5 Y Brainly In




Solve Each Other Pair Of Equation Given Below Using Elimination Method 2y 3 X 12 5y 7 X 1 Mathematics Topperlearning Com D2p1cokk




Elimination Method Day 2 Today S Objective I Can Solve A System Using Elimination Ppt Download




9 X 4 Y 7 2 X Y 4 3y Solve By Elimination Method With Full Solution Brainly In



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions




Level U 2 3x 7y 10 0 Y 2x 3 0 Solde The Following Systems Of Equations 1 11x 15y 23 0 7x 2y




Ukzg6hi0op7fbm




Solve Edl 3 X Y 15 E 2 X 4y Answers 2x Y 7 E9x Y 2x 9 7x 4y 6 E 4x Y 8 X 2y 13 E 5x 14 3y 10 2x 3 12 5y Ci 2y 5x 4 3y 1 8x 5x 2y




2x X Y 6 2 X 2x Y 3 1 Mathematics Topperlearning Com Fqktm544




4 Minutes Warm Up 1 Determine Whether 1 7 Is A Solution Of The System 3x Y 10 X Y 8 2 Solve For X Where 5x 3 2x 1 Ppt Download




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6




Ex 3 6 1 Iii Iv 4 X 3y 14 3 X 4y 23 Ex 3 6




2x Y 4 3y 5x 1 Solve Using Elimination Method Youtube




2x Y 5 0 And 3x 2y 4 0 Find X And Y In Substitution Method And Elimination Method 2 2x 3y 1 And Brainly In




99以上 X Y 5 2x 3y 5 2 3x Y 5 2x 3y 5 X 2y 4y 16
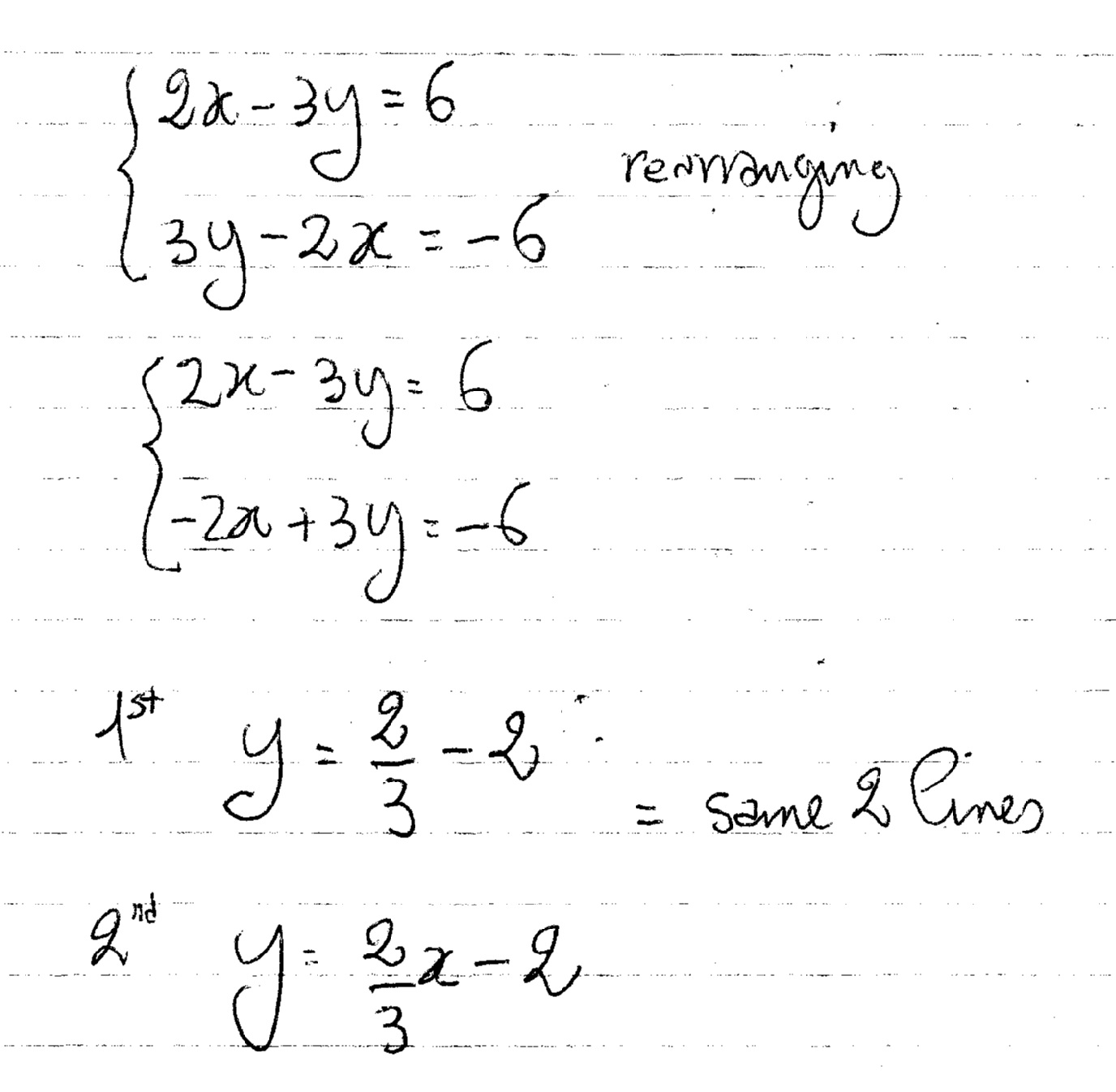



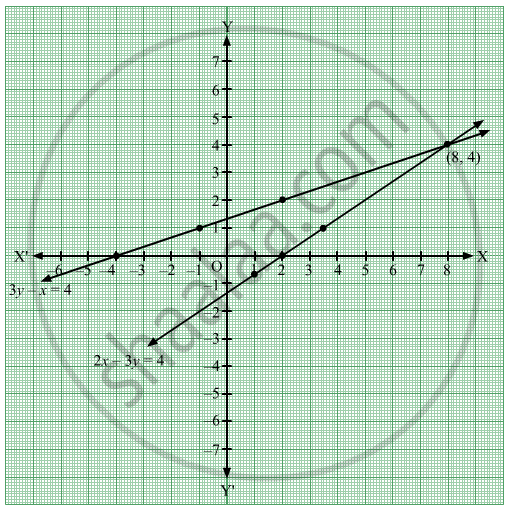
How Do You Solve The System Of Equations 2x 3y 6 And 3y 2x 6 Socratic




2x 3y 1 0 7 4x 3 Y Youtube




Question 1 30 Marks Solve The Following Linear Syst Itprospt




99以上 X Y 5 2x 3y 5 2 3x Y 5 2x 3y 5 X 2y 4y 16




Solved 1 Solve The System Using Substitution Method 2x Y Chegg Com



What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




Solve 2x 3y 11 And 2x 4y 24 And Hence Find The Value Of M For Which Y Mx 3




2x 3y 4 3x Y 5 Solve It By Substitution Method Brainly In



Solve For X And Y 5 X 3 Y 1 3 2x 2 3y 5 Sarthaks Econnect Largest Online Education Community



What Is The Point Of Intersection In The Lines Of 2x 3y 10 And 3x 2y 5 Quora



3x 4y 10 And 2x 2y 2




無料ダウンロード 3x 2y5 X5 Y




Solved 36 X Y 2 3x Y 35 X Y 5 2x Y 12 65 37 2x Chegg Com
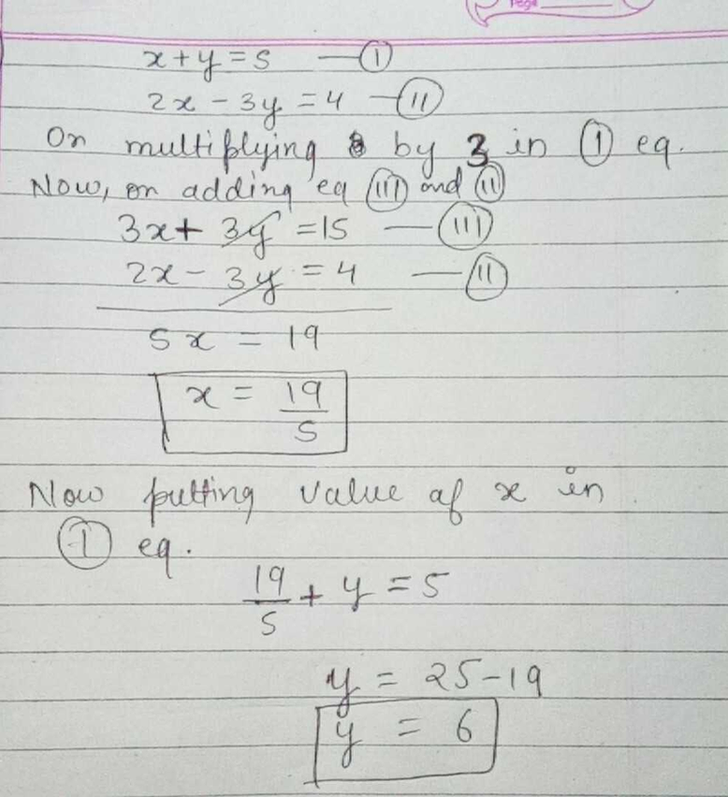



X Y 5 And 2x 3y 4 By Elimination Method Scholr




Solve 2x 3y 4 And 3x Y 5 By Elimination Method Brainly In




Ppt System Of Equations And Elimination Powerpoint Presentation Free Download Id




無料ダウンロード 3x 2y5 X5 Y
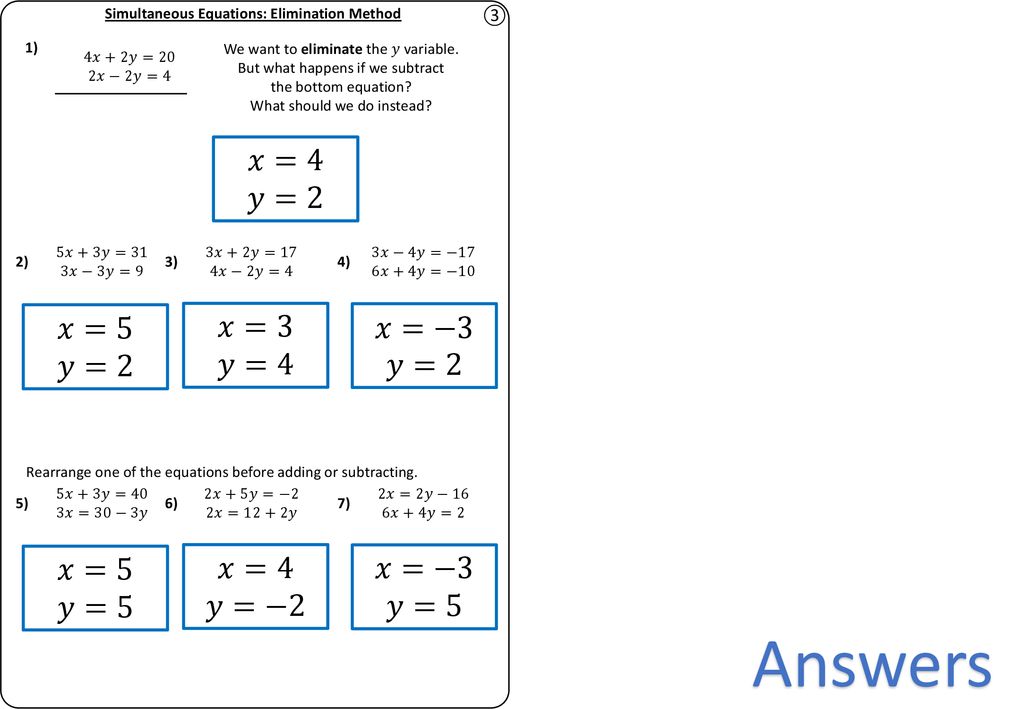



Simultaneous Equations Elimination Complete Lesson Ppt Download




Solve 2x Y 5 And 3x 2y 8




Elimination Method X Y 5 And 2x 3y 4 Youtube




2x 3y 4 3 5x 2y 7 Youtube




Ex 3 3 2 Solve 2x 3y 11 And 2x 4y 24 And Hence Find M For



0 件のコメント:
コメントを投稿